Good Strategy & Bad Strategy

Introducing Richard Rumelt

Friends,

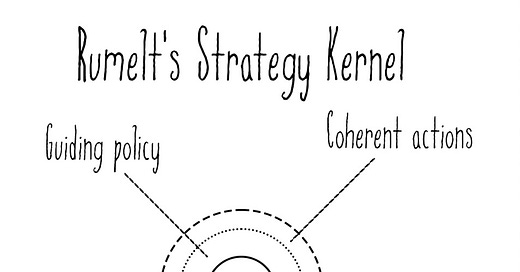
With one theory central to aspiration (the A of ABCDE) in the proverbial books, we today move to the next. In the pantheon of strategic management thinkers, Richard Rumelt unquestionably stands among the all-time greats. Though he may be most known to the broader strategic community for his immensely readable Good Strategy, Bad Strategy, his res…